By Douglas Pinnow
In solving problems, engineers and scientists often begin by drawing a simple figure that shows the various forces and interactions that are relevant. This has been done for the case of a coin moving down-hill on a magnetic slide:
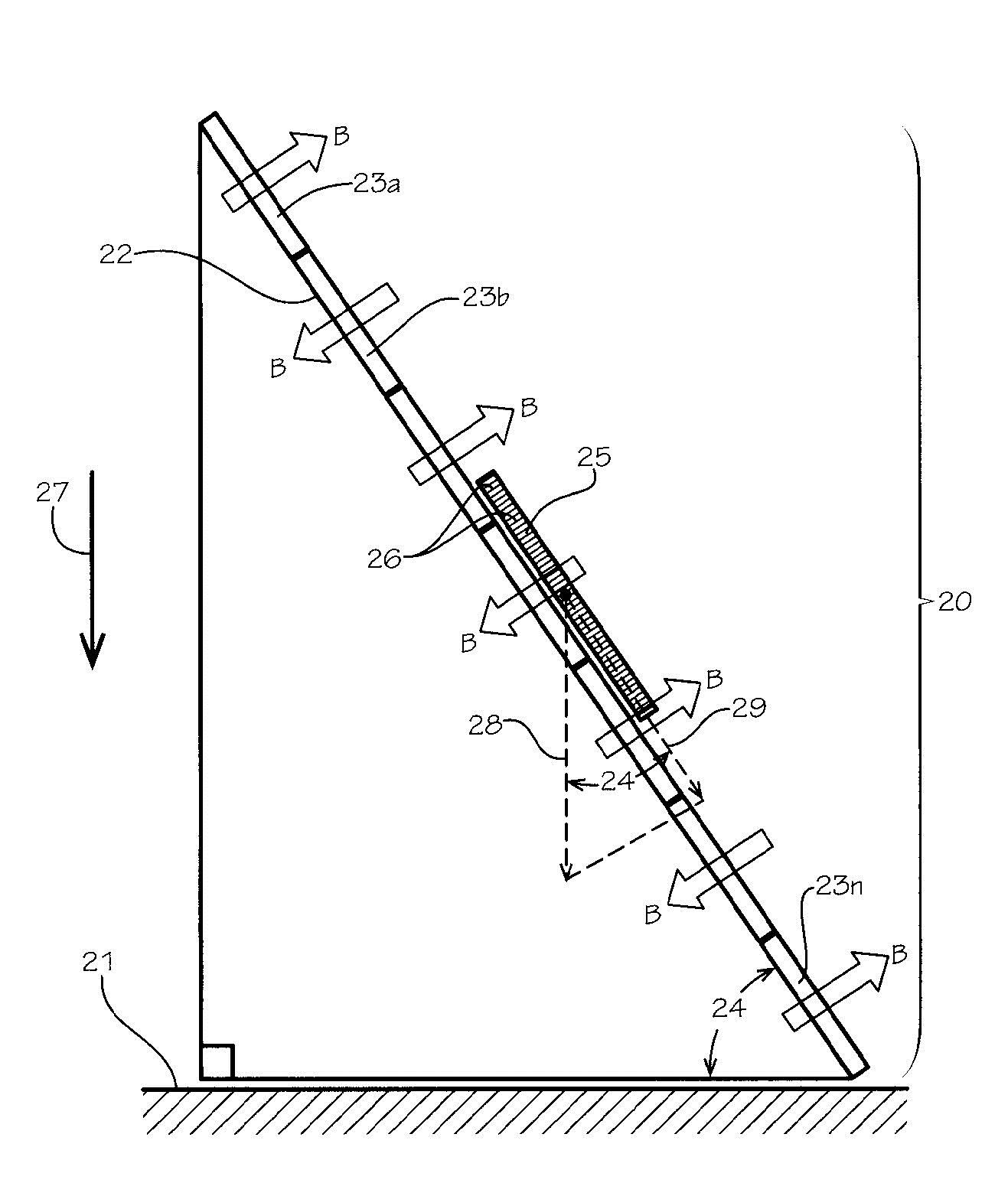
A magnetic side structure 20 is shown resting on a flat horizontal surface 21. The inclined surface 22 is formed by a series of adjacent permanent magnet segments 23a, 23b, 23c,…23n each with a magnet field of magnitude B directed perpendicular to the surface of the inclined plane but alternating in direction above and below the surface of the inclined pane between the said adjacent magnetic segments. The slope angle 24 between the inclined surface and the horizontal surface is also shown in this figure. In this side view drawing, the test coin 25 appears as a rectangular piece with closely spaced reed lines 26 shown on the circular edge of the coin 25. A vertical downward directed arrow 27, to the left of the magnetic slide structure, is a vector representing the acceleration of gravity, g. And force vector 28 represents the downward force acting on the coin having a mass, m. Based on elementary physics, its magnitude, Fg, is the product of m and g. That is:
Fg = mg. (1).
The component of this force vector 29 in the direction down the magnetic slide can be determined by elementary geometry to be:
Fgθ = mg sinθ. (2).
It is also well known the opposing magnetic drag force, FM, is
FM = (constant) (vol.) σBV (3)
where B is the strength of the magnetic field, (vol.) is the volume of the coin 25, σ is the electrical conductivity of the coin’s material, and V is the velocity of the coin 25. The constant in this equation is related to geometric factors that are not significant to this analysis. Since there is no other forces acting on the coin, except a small frictional drag force which is negligible in comparison with the other forces, one can balance the forces on the coin 25 to get the relationship:
FM = Fgθ (4).
Then by substituting equations (2) and (3) into equation (4) and solving for V, one obtains:
V = mg sinθ/[(constant) (vol.) σ B] (5).
As a final step in this analysis, it is helpful to note that the mass, m of the coin 25 is equal to the product of its average density, ρ, and its volume (vol.). That is:
m = ρ (vol.) (6).
When equation (5) and (6) are combined, the (vol.) factors in the numerator and denominator cancel out, leaving the final result:
V= (ρ/σ) g sinθ/[(constant)B] (7).
Importantly, the velocity of a coin on the magnetic slide has a fixed value that is proportional to the ratio of two parameters, ρ and σ, that are basic properties of the coin’s material:
V ~ (ρ/σ) (8)
and inversely proportional the magnetic strength, B:
V ~ B-1 (9).
This fixed velocity is referred to as the “terminal velocity”. It should not be confused with free-fall velocity in the absence of drag.
Although silver has the highest electrical conductivity of any of the elements in the periodic table of elements and therefore [in view of Equation (8)] has a relatively low velocity on a magnetic slide as compared with many other metals, there are several other elements (aluminum, beryllium, magnesium, and copper) that exhibit even lower magnetic terminal velocities, V. So, at first, it did not seem that the performance of silver on a magnetic slide is notable or special. The same appears true for gold.
The above observations concerning silver and gold would tend to suggest that it may not be possible to use their terminal velocity results obtained with a magnetic slide to discriminate pure gold and pure silver from other metals. However, a conceptual breakthrough was made by asking the following question: “Would it be possible for a counterfeiter to find an element or any combination of elements that would have both a blended density and a terminal velocity that would match that of pure gold?”
The non-obvious answer to this question is that no element in the entire periodic table has both a density and a terminal velocity that matches that of gold – or even comes close to such a match. And further, there is no blend of elements in any proportions that could match the density and low terminal velocity of gold. To reach this conclusion requires some considerable effort to evaluate all possible elements with densities greater and less than that of gold that might be combined to match the density of gold and then go on to determine the terminal velocity of each such combination.
This task is somewhat simplified because the rather high density of gold leaves only a limited number of elements for the higher density element component that could be used in such a counterfeiting blend. The choices would be limited to platinum, rhenium, iridium, osmium and/or depleted uranium. And unfortunately for the counterfeiter, a careful analysis shows that there would be no viable choices for a second element of lower density that could be used to make a composite counterfeit material that would simultaneously match both the density and terminal velocity of gold. This is because all five of the above mentioned elements with higher densities than gold also have substantially higher terminal velocities than gold. The closest that a counterfeiter could come to a simultaneous match would be to select iridium as the base metal element with higher density than gold and alloy it with magnesium as the base element with lower density than gold. A density match to gold could be achieved with 92% iridium and 8% magnesium. However, this combination would have a terminal velocity approximately twice that of gold. There is just no possible way to reduce this this high terminal velocity to match that of pure gold. Such a substantial terminal velocity difference between pure gold and the iridium/magnesium counterfeit material would be easy to observe using a magnetic slide. So, the counterfeiter would be out of business, at least in making counterfeit gold coins and bars that did not contain any gold (other than external gold plating) that would pass both a density and terminal velocity test.
However, if the counterfeiter were willing compromise and not attempt to replace all of the gold in counterfeit coin, he/she may think that there might be a chance of succeeding if he/she were to make a counterfeit coin out of an alloy containing, say, 97% gold and 3% silver. It is quite possible that the 3% silver replacement for gold may not make a recognizable difference when the size and weight of such a counterfeit coin were determined. And for the counterfeiter, making a 3% profit might be better than going out of business. However, to succeed, the counterfeiter would have to hope that the addition of 3% silver to the gold alloy would not make a significant change in the velocity on a magnetic slide from that of pure gold. Such a hope would be a serious mistake because Dr. Doug has determined that the addition of 3% (by weight) silver would increase the terminal velocity of the gold alloy by 70%. So, it would be easy to detect such a counterfeit using the magnetic slide.
In time, a smart counterfeiter would learn that the addition of any second metal to gold will substantially increase the terminal velocity of the alloy over that of the pure metal. This is a scientific truth that is known as the “alloy effect” which causes a decrease in the electrical conductivity of alloys due to increased scattering of conductive electrons from a random mixture of different sized atoms within an alloy.
Fortunately, a similar argument can also be made for silver coins and bars. There is no single metal element or combination of elements that could be made that would simultaneously match the density and terminal velocity of pure silver. Molybdenum comes very close to matching the density of silver (10.2 for molybdenum vs. 10. 5 for silver), but silver has a much lower relative terminal velocity (1.0 for silver vs. 3.3 for molybdenum). So, a counterfeit molybdenum coin with silver plating would be easy to spot using a magnetic slide test.
The above discussion forms the basis of the inventive 1-2-3 Method for unambiguously discriminating pure gold and pure silver coins and bars from counterfeit ones. The three steps in this method are:
Step 1. Measure the diameter and thickness of the test coin
(or length, width and thickness of a test bar),
Step 2. Measure the coin’s (or bar’s) weight, and
Step 3. Compare the relative terminal velocity of the test coin
(or test bar) to that of an authentic reference.
The results of Steps 1 and 2, above, can be compared with the corresponding published information and data for investment coins produced and distribute throughout the world. This information is also included with the instructions that come with Dr. Doug’s Test Kit. If there is a match, this establishes that the density of the test coin is proper. Then, if the test coin or test bar has both the correct density and correct terminal velocity on the magnetic slide (as determined in Step 3), one can be assured that it is authentic. Otherwise, it is a counterfeit coin or bar. The conclusion is unambiguous











